
 |
The fitter object provides a nonlinear fitting routine using a standard levenberg-marquardt algorithm. It works similar to the Calculator object: the fitting function is specified in C++ language which is compiled and loaded as a shared object during execution. Therefore the fitting function is executed as native machine code and the fitter provides maximum execution speed. Parameter boundaries can be used for restricting the allowed range of parameter values. Starting values and parameter boundaries can be provided via the property dialog or via connections from outside. The fitting process is monitored with an own viewer window, where also starting values and boundaries can be changed during runtime without creating additional input elements. Together with the fitting function two other functions calculating the individual standard deviation for each datapoint and analytically calculating the derivatives of the fitting function with respect to each parameter. Both are optional and the latter is only for speeding up the fitting process and for greater accuracy.
As output variables the object provides the fitted function in discrete data points,
the parameter values, parameter deviations and chi square function, which is the sum over
the differences between fitted and original function.
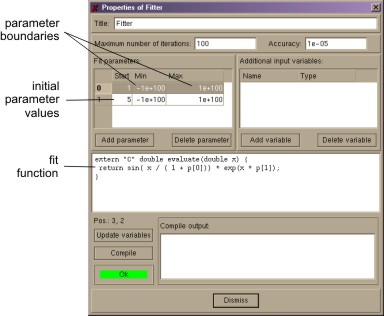
Fig. 1: Property dialog
Figure 1 shows fitter's property dialog. The fitter function must calculate a return value
in dependence on x and the parameters p[0], p[1], .... The number of parameters
used in the fitting function must match the number of parameters given in the "Fit parameters"
box. On the right side additional input variables can be added, which appear as input variables
of the fitter object and can be used within the fitting function or all other functions in the
code window. This for example can be used for doing multidimensional fits.
Starting values of parameters can either be specified alltogether with the AllParameters array or via the float input variables Parameter n..... The latter are useful for example when specifying initial values via scrollbar objects for "visually" creating a good set of initial values by using the "Show only" action.
The fitter object has two actions: "Standard" and "Show only". When calling the standard action, the fitter reads in all connected variables, makes a fit and calculates the resulting function using fitted parameters and the given scale vector. When calling the action "Show only", the fitting process is omitted. This is especially useful for plotting a function generated out of the starting values, which for example can be plotted over the function to be fitted to see whether starting values are useful.
Only when specifying values for sigmas that mach the real measurement accuracy of the fitting function, the individual parameter deviations, that are calculated during the fit, are meaningful.
Example:
When the fitting function is